物性基礎物理学
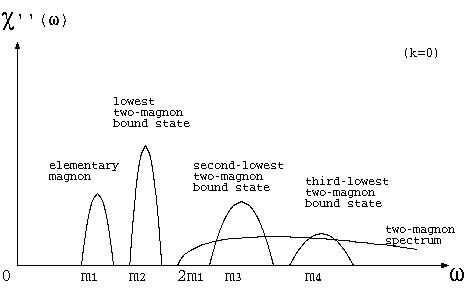
量子統計力学に基づく多体問題の基礎理論、および、その固体電子論への応用を研究する。特に、1体ないしは2体のグリーン関数を数値的に求め、そこから、1粒子の励起構造、あるいは、種々の動的応答関数の性質を把握する。 これらを通して、固体における多体効果の重要性を理解する。さらに、基礎論的な観点から、動的輸送係数や、そのドゥルーデの重みといった非平衡統計力学を研究する。また、これらの相転移点近傍における臨界的特異性を解明する。
|
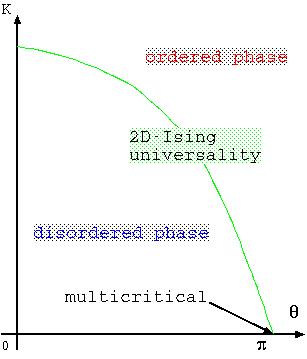
多体問題の数値計算アルゴリズムは、量子モンテカルロ法と厳密対角化法とに大別される。 これらの実用上の特徴は対照的である。ここでは、後者の利点に着目し、虚数磁場下におけるスピン系の協力現象をシミュレーションしている。